Unlocking the Power of Binary Search: Why It’s Efficient and When to Use It

When it comes to searching for a specific value in a dataset, many people rely on brute force methods like linear search, scanning through each element one by one. While this works, it becomes painfully slow for large datasets. Enter binary search, a powerful algorithm that can significantly reduce search time under the right conditions. Let’s dive into why binary search is so efficient, when to use it, and other considerations you might be overlooking.

How Binary Search Works

Binary search operates on a simple principle: divide and conquer. Instead of iterating through each element, the algorithm continuously splits the dataset in half until the target value is found (or the search space is exhausted). Here’s a quick breakdown of how it works:

1. Start with two pointers: one at the beginning (left) and one at the end (right) of the sorted array.
2. Calculate the middle index (mid) of the current range.
3. Compare the value at mid with the target:
   • If it matches, return the index.
   • If the target is smaller, narrow the search to the left half (right = mid - 1).
   • If the target is larger, narrow the search to the right half (left = mid + 1).
4. Repeat until the target is found or the pointers overlap.

Key Takeaway: Each step cuts the search space in half, making binary search extremely fast for large datasets.

Why Binary Search is Efficient

The efficiency of binary search stems from its time complexity, which is $O(\log n)$. This means the number of steps required grows logarithmically as the size of the dataset increases. Let’s put that into perspective:

• For an array of 16 elements, binary search requires at most 4 steps.
• For an array of 1,000,000 elements, it needs around 20 steps.
• Compare this to linear search, which may need up to 1,000,000 steps for the worst-case scenario!

This efficiency makes binary search ideal for large datasets where quick lookups are critical.

Key Benefits of Binary Search

1. Speed on Sorted Data:
   • Binary search is much faster than linear search, but it requires the array to be sorted beforehand.
2. Minimal Memory Overhead:
   • With a space complexity of $O(1)$, binary search uses only a handful of variables (left, right, mid) regardless of the array size.
3. Simplicity:
   • The algorithm is straightforward and easy to implement in most programming languages.

Limitations of Binary Search

Despite its advantages, binary search isn’t a one-size-fits-all solution. Here are some caveats to consider:

1. Requires Sorted Data:
   • Binary search only works on sorted datasets. If your data isn’t sorted, you’ll need to sort it first, which adds a time complexity of $O(n \log⁡ n)$.
2. Not Dynamic:
   • If your dataset is frequently updated (e.g., insertions or deletions), you’ll need to re-sort it before performing a binary search. This can be costly in dynamic scenarios.
3. Exact Matches Only:
   • Binary search works best when you’re searching for a specific value. If you need to find approximate matches, ranges, or complex conditions, other data structures (like binary search trees) might be better suited.

When to Use Binary Search

Binary search is an excellent choice in scenarios where:

• The data is static and sorted. For example, a list of usernames or product IDs that don’t change frequently.
• Memory efficiency is crucial, as it avoids the overhead of hash tables or additional data structures.
• Exact value lookups are required.

Beyond the Basics: Other Considerations

While binary search is powerful, you may need to account for additional factors:

1. Handling Edge Cases:
   • Make sure your implementation correctly handles duplicate values, empty arrays, or scenarios where the target isn’t found.
2. Floating-Point Arithmetic:
   • For datasets involving floating-point numbers, rounding errors can occur. Use appropriate precision handling.
3. Variants of Binary Search:
   • First/Last Occurrence: Modify the algorithm to find the first or last occurrence of a value in a sorted array with duplicates.
   • Closest Value: Adapt binary search to find the value closest to the target.
4. Alternative Data Structures:
   • If your dataset is dynamic, consider using binary search trees or hash maps, which can offer more flexibility for frequent updates.

The JavaScript Implementation

Here’s the basic implementation of binary search in JavaScript:

function binarySearch(arr, target) {
    let left = 0;
    let right = arr.length - 1;

    while (left <= right) {
        const mid = Math.floor((left + right) / 2);

        if (arr[mid] === target) {
            return mid;  // Target found
        } else if (arr[mid] < target) {
            left = mid + 1;  // Search the right half
        } else {
            right = mid - 1;  // Search the left half
        }
    }

    return -1;  // Target not found
}

How to Use It

Now that we have the binarySearch function, let’s see how to use it:

// Example dataset (must be sorted for binary search to work)
const arr = [1, 3, 5, 7, 9, 11, 13, 15];

// Example target value
const target = 7;

// Call the binarySearch function
const index = binarySearch(arr, target);

// Output the result
if (index !== -1) {
    console.log(`Target ${target} found at index ${index}`);
} else {
    console.log(`Target ${target} not found`);
}

Sample Output

Target 7 found at index 3

In this example, we search for the number 7 in the sorted array. The binary search efficiently finds its index, which is 3.

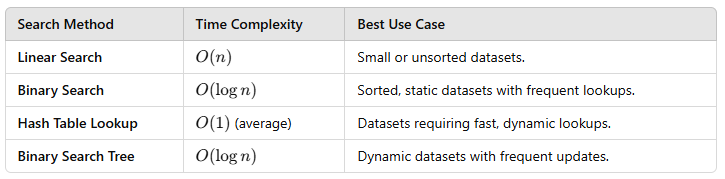
How Does Binary Search Compare to Other Approaches?

Final Thoughts

Binary search is a foundational algorithm that every developer should have in their toolkit. Its efficiency, simplicity, and versatility make it ideal for scenarios where data is sorted and static. However, it’s essential to understand its limitations and weigh them against your specific requirements.

Support Us